Next: Sobre Machos e Fêmeas Up: Parasitismo e Predação Previous: O Inimigo Interior Sumário
Enquanto a maioria das teorias adaptacionistas busca explicar a uniformidade do código genético, [Krakauer and Jansen(2002)Krakauer & Jansen] procuraram explicar os aspectos divergentes, i.e., o mapeamento entre codon e anticodon e entre anticodon e aminoácido, assumindo que o código evolui em um ambiente com um risco constante de parasitismo traducional (um vírus seria um exemplo contemporâneo de um parasita traducional).
A redundância de anticodon refere-se a casos onde anticodons idênticos podem reconhecer diferentes codons para traduzir em um aminoácido, enquanto que a degenerescência de anticodon envolve diferentes anticodons reconhecendo diferentes codons para traduzir em um aminoácido Krakauer02.
Os modelos propostos por [Krakauer and Jansen(2002)Krakauer & Jansen] ilustram como mudanças na redundância e degenerescência de anticodon devem modificar as taxas de replicação de parasitas e como a dinâmica populacional parasita-hospedeiro influencia a tradução, conforme a hipótese da Rainha Vermelha. [Krakauer and Jansen(2002)Krakauer & Jansen] encontraram que em populações assexuadas, tanto monomórficas quanto polimórficas, parasitas podem promover a diversidade do processo traducional per se.
Vamos considerar um modelo de tradução de um par de codons sinônimos por um par de anticodons em um único aminoácido. Este modelo, bem como uma generalização para conjuntos maiores de codons, foi desenvolvido por [Krakauer and Jansen(2002)Krakauer & Jansen].
Sejam dois codons que codificam para o mesmo aminoácido e dois
anticodons com ocorrências relativas dadas por ![]() e
e
![]() . Suponha que um parasita pode usar dois codons diferentes
com ocorrências relativas dadas por
. Suponha que um parasita pode usar dois codons diferentes
com ocorrências relativas dadas por ![]() e
e ![]() . Ambos
os codons podem ligar-se a ambos os anticodons, mas com diferentes
afinidades. A afinidade do codon
. Ambos
os codons podem ligar-se a ambos os anticodons, mas com diferentes
afinidades. A afinidade do codon ![]() pelo anticodon
pelo anticodon ![]() é dada por
é dada por ![]() ,
se
,
se ![]() , ou por
, ou por ![]() , se
, se ![]() ,
, ![]() .
.
A taxa total de ligação do codon 1 é dada por
![]() e a do codon 2 é dada por
e a do codon 2 é dada por
![]() .
O tempo médio que demora para o codon
.
O tempo médio que demora para o codon ![]() ser encontrado é dado por
ser encontrado é dado por
![]() . Se
. Se ![]() é o tempo gasto para iniciar o processo de
tradução, o tempo total da tradução é dado por
é o tempo gasto para iniciar o processo de
tradução, o tempo total da tradução é dado por
| (1) |
Assumindo que a extensão da proteína é o passo limitante, e não a
remoção de anticodons impropriamente ligados, a taxa de tradução é dada
por ![]() . Ou seja, a taxa de extensão de um único aminoácido é
dada por
. Ou seja, a taxa de extensão de um único aminoácido é
dada por
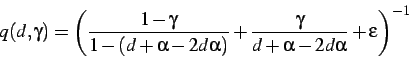 |
(2) |
A única variável que o parasita pode alterar é ![]() . Quando tudo o
mais é fixo, podemos encontrar que valores de
. Quando tudo o
mais é fixo, podemos encontrar que valores de ![]() maximizam o taxa
de tradução. Encontramos
maximizam o taxa
de tradução. Encontramos
| (3) | |||
| (4) |
Isto mostra que pequenos desvios nas afinidades pelos codons resultam no uso exclusivo pelo parasita dos codons favorecidos. O hospedeiro pode variar não só a utilização dos codons, mas também a matriz de afinidade ou a abundância dos anticodons. Contudo, a utilização dos codons também determina a taxa de erro durante a transcrição Krakauer02.
Vamos tratar agora da dinâmica de populações. Seja ![]() a abundância de
hospedeiros e
a abundância de
hospedeiros e ![]() a de parasitas. Assumimos que a infecção é
proporcional à taxa de tradução. Além disso, assumimos que a taxa de
replicação do hospedeiro não depende da taxa de tradução de seus
próprios genes Temos, então,
a de parasitas. Assumimos que a infecção é
proporcional à taxa de tradução. Além disso, assumimos que a taxa de
replicação do hospedeiro não depende da taxa de tradução de seus
próprios genes Temos, então,
Assumimos que hospedeiros e parasitas são completamente antagonistas e a
transmissão dos parasitas é horizontal. As dinâmica de população deste
modelo são bem conhecidas; as densidades apresentam oscilações neutras
estáveis em torno do equilíbrio. As densidades médias dos hospedeiros e
parasitas ao longo destas oscilações são iguais às respectivas
densidades de equilíbrio. As abundâncias de equilíbrio são dadas por
| (7) |
Então, um aumento na taxa de tradução leva a uma concomitante redução na abundância tanto de parasitas como de hospedeiros. Uma redução na taxa de tradução dos genes do hospedeiro leva uma redução na abundância de parasitas sem nenhum impacto na abundância dos hospedeiros.
Agora vamos reunir o modelo com um modelo de dinâmica de populações.
Consideraremos o destino de hospedeiros mutantes com uma redundância
diferente. Assumimos que uma mudança na redundância é alcançada por uma
mudança em ![]() (a redundância é mínima quando
(a redundância é mínima quando ![]() ou
ou ![]() e máxima
quando
e máxima
quando ![]() ). A afinidade dos mutantes será denotada por
). A afinidade dos mutantes será denotada por ![]() .
Consideraremos também parasitas mutantes com utilização dos codons dada
por
.
Consideraremos também parasitas mutantes com utilização dos codons dada
por ![]() .
.
Se um hospedeiro mutante é raro, será predominantemente infectado por
parasitas residentes, da mesma forma que parasitas mutantes raros
infectarão predominantemente hospedeiros residentes. A dinâmica dos
hospedeiros e parasitas residentes é aproximadamente dada por
(![]() ) e (
) e (![]() ), supondo que os mutantes são raros.
A dinâmica de hospedeiros mutantes raros
), supondo que os mutantes são raros.
A dinâmica de hospedeiros mutantes raros ![]() e parasitas mutantes
raros
e parasitas mutantes
raros ![]() é dada por
é dada por
| (8) | |||
| (9) |
Estas expressõem mostram que a evolução dos hospedeiros maximiza a densidade de parasitas enquanto que a evolução dos parasitas minimiza a densidade de hospedeiros.
Pode-se deduzir uma dinâmica evolucionária para ![]() e
e ![]() . Seja
. Seja
![]() a taxa de mutação média do hospedeiro e
a taxa de mutação média do hospedeiro e ![]() a do
parasita. Obtemos, então,
a do
parasita. Obtemos, então,
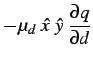 |
(10) | ||
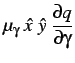 |
(11) |
Uma simulação revela uma corrida armamentista sem fim, de acordo com a hipótese da Rainha Vermelha (Figura 1). A dinâmica evolucionária cíclica faz a redundância flutuar entre valores extremos (Figura 2).
Leonardo 2003-12-20